如果，我们研究年龄对肿瘤患者的影响，叫做相关分析；如果，我们研究年龄对肿瘤患者死于心血管疾病的影响，又应该叫做什么呢？比如我最近读的这篇文章，来自JAMA Cardiology

再比如说，我想研究A方案与肺癌复发的关系，但是如果病人有心理问题，自杀了，也就观察不到肺癌的复发，也就是说自杀与复发之间存在竞争关系，这样的想象在医学研究中非常常见，你想研究A方案导致病人死亡，可是现实却是病人因为B原因死亡，这个就是竞争风险模型。

这么说似乎不够学术，那么咱们来个学术点的定义。

竞争风险模型( Competing Risk Model ) : 指的是在观察队列中，存在某种已知事件可能会影响另一种事件发生的概率或者是完全阻碍其发生,则可认为前者与后者存在竞争风险。而上述的患者死于肺癌还是死于自杀，就是竞争风险事件。

在小黑屋之前的课程中，我们学习过生存分析（survival analysis），其中描述分析可以使用（Kaplan-Meier法），描述不同组患者的生存时间及生存状态。传统的生存分析关系的结局是一个终点时间，不存在竞争风险（即我们关心的是患者到随访结束是生存还是死亡。）

竞争风险模型适用于多个终点的生存数据，是一种处理多种事件的统计学方法，早在 1999 年 Fine 和 Gray 就提出了部分分布的半参数比例风险模型，在竞争风险模型中有很多重要的概念，而我们最常使用的是累计发生率函数（Cumulative Incidences Function , CIF ）

竞争风险  作图展示

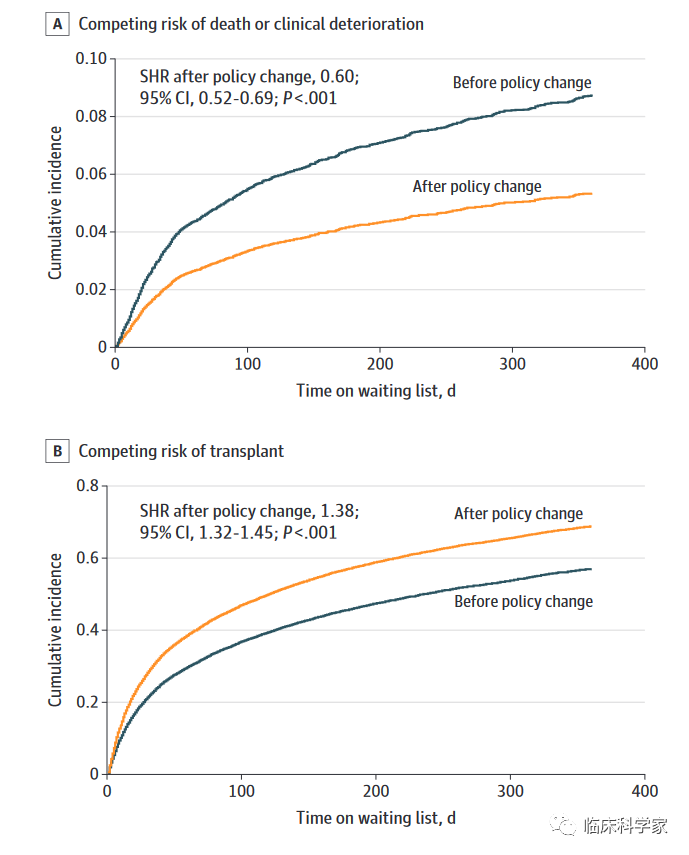
图片来自于Evolving Trends in Adult Heart Transplant With the 2018 

Heart Allocation Policy Change, IF: 14.676

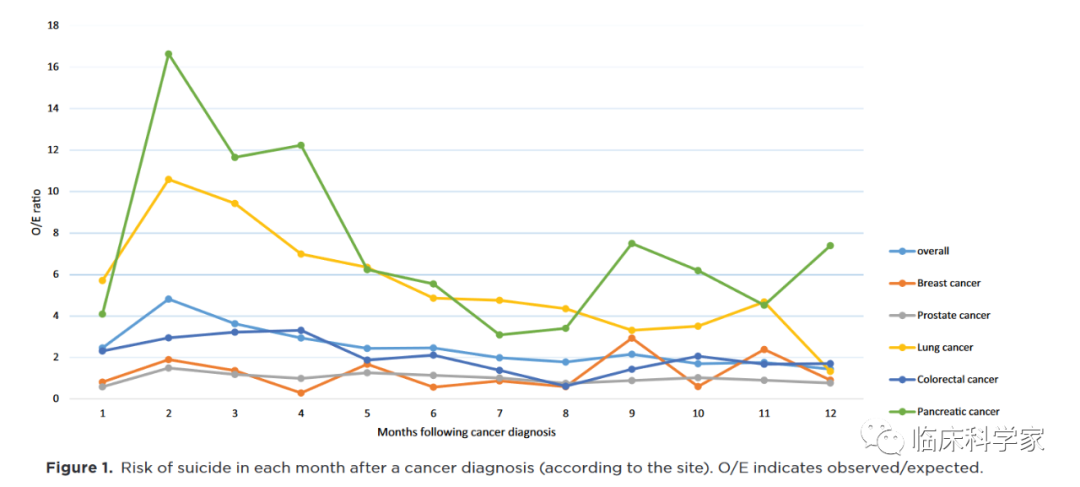
图片来自于Suicidal Death Within a Year of a Cancer Diagnosis: 

A Population-Based Study, IF: 6.86

数据示例  一起动手，小编找到一组数据：

R语言自带关于竞争风险模型的数据（bmtcrr），点击链接打开http://www.stat.unipg.it/luca/R/，找到竞争风险模块，即可下载数据。大家可以动手操作一下哦！

本案例数据是探讨骨髓移植对比血液移植治疗白血病的疗效，结局事件定义为 “复发”，某些患者移植后不幸因为移植不良反应死亡，那这些发生移植相关死亡的患者就无法观察到“复发” 的终点，也就是说 “移植相关死亡” 与“复发”存在竞争风险。故采用竞争风险模型分析。

可以利用以下代码，使用R来快速跑一下竞争风险模型，领略一下吧！

bmtcrr竞争风险R代码

library(foreign)

bmt<-read.csv('bmtcrr.csv') ##从当前工作路径中导入数据

str(bmt)  ##显示数据

 

library(cmprsk)  ##加载竞争风险程序包

bmt$D <- as.factor(bmt$D) ##加载数据框 bmt，并定义结局为因子变量

attach(bmt)

 

##使用 cuminc() 函数进行单因素的 Fine-Gray 检验

fit1 <- cuminc(ftime,Status,D)

fit1

plot(fit1,xlab = 'Month', ylab = 'CIF',lwd=2,lty=1,

     col = c('red','blue','black','forestgreen'))

 

cov <- data.frame(age = bmt$Age,

     sex_F = ifelse(bmt$Sex=='F',0,1),

     dis_AML = ifelse(bmt$D=='AML',0,1),

     phase_cr1 = ifelse(bmt$Phase=='CR1',0,1),

     phase_cr2 = ifelse(bmt$Phase=='CR2',0,1),

     phase_cr3 = ifelse(bmt$Phase=='CR3',0,1),

     source_PB = ifelse(bmt$Source=='PB',0,1)) ## 设置哑变量

#cov

fit2 <- crr(bmt$ftime, bmt$Status, cov, failcode=1, cencode=0)

summary(fit2)

数据分析  结果解读

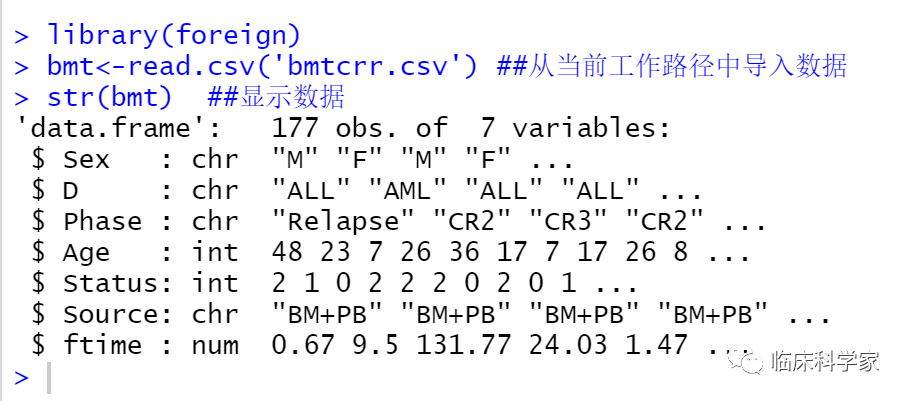
结果运行到这里，那么我们分析这些数据到底是什么意思，

Test之后，有两个统计数据分别是  2.86, P=0.09, 表示在控制了竞争风险事件（即第二行计算的统计量和 P 值）后，“ALL”和“AML” 累计复发风险之间无统计学。

$est 及$var分别表示估计的各时间点“ALL” 和“AML”组的累计复发率与与累计竞争风险事件发生率和方差。

当然光有数字是不够的，我们还需要作图。

 

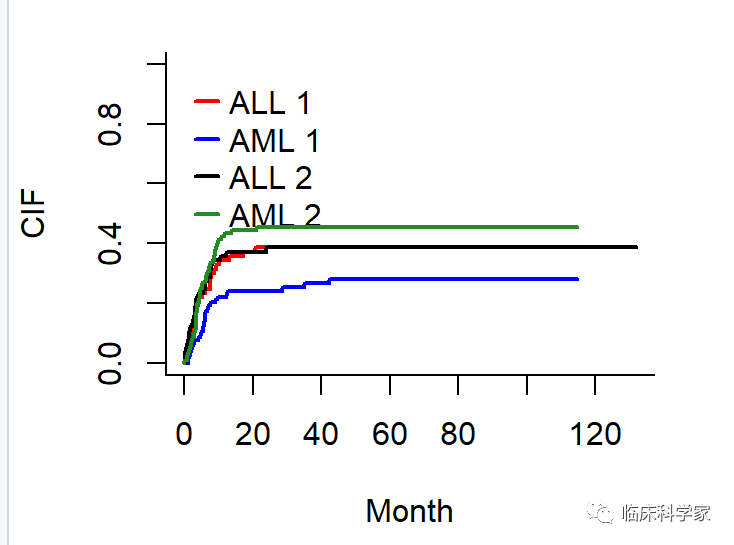
在这个图中，纵坐标表示累计发生率 CIF，横坐标代表的是月份即时间轴。我们从这个图可以发现在前17月里，四条曲线基本重合，而且从前面的数据也可以看出来P值没有差别，也就是这两组患者的累计复发风险明显明显统计学差异。

在小黑屋中，我们反复强调四图四表中的单因素与多因素分析，那么可不可以在R里面实现竞争风险事件的生存资料的多因素分析呢？答案当然是：可以！

cov <- data.frame(age = bmt$Age,

sex_F = ifelse(bmt$Sex=='F',0,1),

dis_AML = ifelse(bmt$D=='AML',0,1),

phase_cr1 = ifelse(bmt$Phase=='CR1',0,1),

phase_cr2 = ifelse(bmt$Phase=='CR2',0,1),

phase_cr3 = ifelse(bmt$Phase=='CR3',0,1),

source_PB = ifelse(bmt$Source=='PB',0,1)) ## 设置哑变量

#cov

fit2 <- crr(bmt$ftime, bmt$Status, cov, failcode=1, cencode=0)

summary(fit2)

结果解读：

在控制了竞争风险事件后，相对于参照组，CR1, CR2, CR3 的累计复发风险，HR 及 95% CI 分别为 3.009(1.439,6.29), 2.773(1.381,5.57), 2.078(0.67,6.43), 对应的 P 值分别为 0.0034, 0.0041, 0.2000。

总结：

竞争风险模型针对的是结局事件并非二分类变量，近年来关于seer数据库的文章中得到广泛的应用，在风锐中也可以将患者分为死于癌症（结局事件），或者死于其他（删失和竞争风险事件）来绘制KM曲线，本文主要使用 R 的 cmprsk 程辑包进行 Fine-Gray 检验与竞争风险模型及累计风险率的计算，可以观察患者在控制竞争风险事件后，患者的累计风险率是否存在差异。同时必须指出的是，选择什么样的模型进行分析，必须基于自身的数据类型以及结局是否存在竞争风险，它与cox模型并不存在优劣，可以互为补充。