在临床试验中，往往因物理或人为因素造成数据缺失，即使是少量的缺失值，也可能对试验结果带来偏倚，进而影响研究结果的准确性和可靠性。针对此问题，诸多学者陆续提出了一系列处理缺失值的方法，而这些方法亦有各自的适用背景和前提假设[1-5]。但部分临床研究未根据缺失值类型采取相应的正确处理方法，更有甚者将本不应剔除的缺失数据直接删除，这些操作直接导致了临床试验中缺失值的处理不当和报告不规范。因此，本文阐述临床试验中常见缺失值类型及其处理方法，旨在提高研究人员对缺失值的认识，减少其处理方法的误用，进而提高临床试验结论的可靠性与有效性。

1 缺失值介绍

1.1  基本概述

缺失值是指因物理或人为等原因未能采集到的试验相关数据。造成数据缺失的原因主要包括：

1

未严格规范研究设计、数据采集和质量控制，如从医院病案系统调取数据时操作不当；

2

因设备故障或研究人员个人疏忽而无法收集完整的试验数据，如因数据存储硬件出现故障而导致数据缺失；

3

参与者的个人原因，如出于安全考虑或试验给参与者造成不便而退出试验、因担心涉及敏感信息而拒绝参与调查、因搬迁而失访等。

即使试验前已制定了严格的研究方案和规范的处理流程，但试验过程中仍会因各种不可预测因素导致数据缺失[6]。如针对发表于高水平杂志的77个临床随机对照试验的系统回顾研究发现，高达95%的试验存在不同程度的数据缺失[7]。

1.2 重要意义

在临床研究中，科学、合理地收集和管理原始数据是研究可靠性、真实性的重要保证[8]。缺失值的存在降低了所包含样本的群体代表性，减弱了临床试验的优势，降低了试验的把握度，引入了潜在偏倚，影响试验结果的解释性和可信度。在临床实践中，研究者往往直接忽略缺失数据的参与者，仅纳入完整数据的参与者进行分析，即采用完整案例分析（complete-case analysis）。而此方法可导致样本量削减、破坏原有的组别间平衡、引入偏倚，进而损害试验结果的稳健性与准确性。因此，如何科学、合理地处理缺失值是临床试验中不可忽视的问题。

2 数据缺失的机制

应对策略的选择取决于对数据缺失机制的假设，因此了解数据缺失的机制类型非常必要。Lazar等[9]提出了数据缺失的分类方法，根据其研究结果可将数据缺失机制类型分为：完全随机缺失（MCAR）、随机缺失（MAR）和非随机缺失（MNAR）。

2.1 完全随机缺失

MCAR是指参与者的数据缺失是随机发生的，完全独立于已观测和未观测到的数据，因此MCAR数据可视为试验数据集里的一个随机子集。如研究人员因当天试验检测设备故障、无法正常收集试验结果而造成数据缺失，这种由随机因素引起的数据缺失被归类为MCAR。值得注意的是，此种机制假设性较强，且往往难以进行有力验证。若无法满足MCAR的强假设条件，将缺失值全部按照MCAR机制处理是不可取的。

目前，Heymans 等[10]指出，两种方法可辅助判断缺失值是否为MCAR机制，一种方法为t 检验和逻辑回归分析法，另一种方法为Lazar等[9]提出的MCAR检验法。t 检验可比较非响应者组与响应者组之间的差异，若缺失值指示变量对应的P值不显著，则可能为MCAR机制。逻辑回归分析可检验缺失值指示变量对感兴趣变量的预测作用，若回归系数不显著，则可能为MCAR机制。两种方法结合使用可初步判断缺失值是否为MCAR机制。MCAR检验法通过比较每个缺失数据模式下变量的实际观察均值与使用最大期望（EM）算法估计的预期总体均值之间的差异判断缺失值是否属于MCAR机制。若这些差异在各个缺失数据模式下均很小且无显著性，可认为是MCAR机制。反之，若差异较大或存在显著性，则可能不是MCAR机制。

2.2 随机缺失

MAR是指缺失数据仅关联于参与者已观测到的变量值，是临床试验中最常见的缺失机制，当控制了与MAR关联的已观测到的变量后，可认为此缺失数据与未观测到的变量不相关。如一项针对中老年人控制血糖的临床研究中，某高龄组参与者认为该干预措施造成其生活不便而退出临床试验，进而导致数据缺失。在此情况下，可认为年龄（作为一个已观测到的变量）是导致数据缺失的重要原因，数据的缺失机制可考虑为MAR；当控制了年龄这一变量后，可认为数据缺失与未观测到的变量并无关联。然而，与MCAR机制类似，当前难以根据定义或数据本身评估缺失数据是否为MAR机制，在实际工作中对于MAR的判断比MCAR难度更大[10]。

2.3 非随机缺失

MNAR又称不可忽略的缺失（NIM），被定义为试验数据出现缺失的概率与参与者未观测到的变量相关。如一项关于药物治疗抑制肿瘤生长的临床试验中，参与者在前几次随访时均展现出理想的治疗效果，但在下一次随访前突然病情恶化而退出试验，导致数据缺失，而此种情况导致的数据缺失机制即为MNAR。

通常情况下，当无法判断数据缺失是MCAR或MAR时，可认为其为MNAR并进行相应处理，或作敏感性分析以辅助评估对数据缺失机制假设的稳健性及可靠性。但实际上，即使可通过比较分析或构建模型以区分MCAR与MAR，当前依然无法准确判断缺失数据属于MAR还是MNAR。对于MNAR与MAR的区分，仍主要依赖于临床科研工作者的专业判断，且只能在某种程度上“猜测”缺失数据是否属于MNAR。

3 缺失值的常见处理方法

缺失值的处理方法总体上可分为删除法、插补法和逆概率加权法（IPW）。常见处理方法的优点、缺点及适用条件详见表1，部分处理方法应用实例详见表2。

表1 缺失值的常见处理方法

表2 缺失值常见处理方法应用实例

3.1 删除法

在不考虑缺失数据对临床试验结果影响的情况下，直接在已获取的试验数据集上进行处理分析，可使用删除法。删除法包括列表删除（listwise deletion）和成对删除（pairwise deletion）。

3.1.1　列表删除

处理缺失数据最简单的方法是直接删除含有缺失数据的参与者个案，分析试验数据集中剩余的完整数据，这种方法称为列表删除或完整案例分析，当缺失数据类型为MCAR时，且缺失数据很少（通常认为少于总体数据的5％）[17]，可选用列表删除。表2中Rautenberg等[11]应用了列表删除法处理缺失值，操作简单、易行。该方法的优点在于操作简单，无需人为填补数据。不足之处在于，当样本量较少且缺失数据比例较高时，列表删除可造成大量信息损失，影响样本的客观性和统计效能。此外，当数据不满足MCAR假设时，这种处理方法可引入潜在偏倚。故列表删除适用于MCAR条件下，样本量较大且缺失值较少的场景。

3.1.2　成对删除

成对删除也称为可用案例分析（available-case analysis），是指进行多个变量分析时，根据分析需要仅删除所分析变量的缺失数据，无需将此案例完全删除。相较于列表删除，该方法更大限度地保留了试验数据集中的可用信息。

值得注意的是，由于不同分析所涉及的变量不一样，其有效样本量也会不断发生变化。故此方法适用于MCAR条件下，关键分析变量缺失较少的场景。Sayasone等[12]探究三苯双脒与吡喹酮的疗效和安全性时应用了成对删除（表2），即针对不同结局的分析而删除无需参与分析变量的缺失数据。

3.2 插补法

在临床试验中，为了使试验结果更具准确性和可靠性，减少缺失值对整个试验的不良影响，除可使用删除法外，还有一种更常见的方法——插补法。插补法是指用合理的数值填充缺失数据的做法，即对缺失值进行预测，用一些替代值填补缺失的数据，采用填补后的完整数据集进行后续统计分析，而这些替代值被称为插补值。在满足相应缺失机制要求的情况下，插补法可有效解决数据缺失问题，不必担心因排除数据缺失个案而导致数据分析不完整。目前，常用的插补法包括单一插补（single imputation）、多重插补（MI）、基于模型插补（model-based imputation）。

3.2.1　单一插补

单一插补是指采用一定的方法构造一个恰当合理的预测值，填充缺失的数据元素。目前，广泛使用的单一插补方法有均值插补、末次观测值结转法（LOCF），以及最差观测值结转法（WOCF）。

1 均值插补

即计算每个变量已有观测值的平均值，并通过均值填补该变量的缺失值。均值插补通常应用于MCAR类型，并适用于缺失值较少且无明显规律的连续性数据。一般情况下，当变量服从正态分布时，可将此变量的平均值作为插补值；若变量不服从正态分布，则可考虑将变量的中位数或众数作为其插补值。如Menendez等[13]在临床试验研究中，应用均值插补方法填充8项变量缺失的数据，构成一个完整的数据集，方便后续进行结果分析（表2）。

在合理应用于MCAR机制情况下，均值插补的优点在于简单、方便，然而其缺点是人为减少变量的变化，可能人为造成对研究误差的错误低估，错误高估效应量的精度，也忽视了插补变量与其他观察变量的相关性，可能引起处理后的数据方差与实际方差不同的问题。使用均值插补法时，需谨慎评估其在特定数据集中的适用性和局限性。

2 末次观测值结转法

LOCF是指在纵向研究（即按时间点对每位受试者采取重复措施的试验）中插补缺失数据的方法，缺失的后续测量值均由观察到的最后一次测量值替代，适用于MCAR类型。

Witkiewitz等[14]的研究应用了LOCF处理缺失值，收集退出治疗前可获得的所有饮酒数据，使用最后1个月的饮酒数据替代治疗退出后缺失的测量值。LOCF可减少因某次失访而造成患者的脱落偏倚。需注意的是，此方法的使用前提是假设研究对象的情况在脱落或失访后仍保持不变，但这种假设在临床研究中较难满足，因为受试者常表现出某种趋势[18]。因此，指南建议尽量避免使用LOCF方法作为主要方法（除非所依据的假设在科学上是合理的），并鼓励使用其他替代方法处理缺失数据[1]。

3 最差观测值结转法

WOCF是指用试验中已观测到的最坏情况的参与者数据去填补缺失值，一般适用于MCAR类型。在实际工作中，WOCF常用于因缺乏疗效而使参与者脱落试验的情况，可对药物疗效进行保守评价，临床上也将这种试验设计方法称为缺乏疗效设计。

此外，单一插补方法还包括基线观测结转、回归插补、EM算法填充、热层填补、冷层填补、回归（Buck方法）等[19]。尽管单一插补方法多样，简单易行，但多数方法仅在MCAR条件下为总体均值或总量提供无偏估计。单一插补中估计的插补值通常有偏于实际观测值（比实际观测值高或低），且此方法使得插补值集中于某一点（如均值）上，在缺失数据比例较大时将影响填补后的数据分布，导致方差被低估，影响效应量的正确估计，从而降低试验结果的精度。

3.2.2　多重插补

MI是在单一插补的基础上衍生而来，最早由哈佛大学的Rubin教授于1977年提出[20]，目前广泛应用于临床试验中缺失值的处理。MI的理论基础是贝叶斯估计，被定义为在数据类型为MAR的情况下，用多个合理的随机值替换缺失数据，从而创建多个完整的数据集进行分析，并将结果合并。因此，MI包含3个阶段，即插补阶段、分析阶段及结果合并阶段，每个阶段均考虑了缺失值的不确定性（图1）。

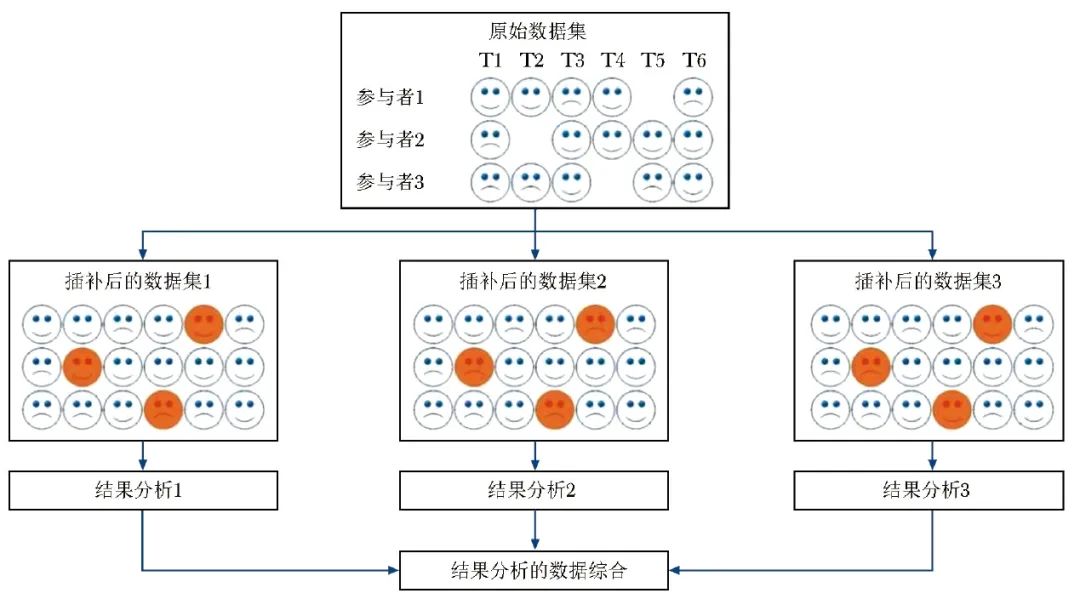
图1 多重插补流程图

具体而言，在插补阶段，MI生成原始数据集的多个“副本”（即插补后的完全数据集），而在每个完全数据集中，缺失的数据从反映观测数据概率分布中随机抽取的值进行插补。因此，在第一阶段插补过程中，通过随机生成多个“副本”数据集以考虑插补值的不确定性。

在分析阶段，拟合模型并估计每个已插补数据集的结果效应值。在每个试验数据集中，已观测到的数据保持不变，由于使用不同的估算方法，不同插补值的变化可产生不同的效果估计。不同的插补值反映了估计模型的不确定性，而不仅仅是添加了不同的“残差”。

最后，在结果合并阶段，将所有效应估计值汇集在一起，将所有已插补数据集的平均效应估计值作为点估计值，同时通过合并插补数据集内部和数据集之间的变异计算标准误[21]。

Witkiewitz等[14]在一项针对酒精依赖性治疗的临床试验中，比较纳曲酮与安慰剂在酒精依赖性患者中的治疗效果，应用多重插补法处理缺失值，创建了50个不同的填补后数据集，汇总估计这些填补后数据集的效应值。

MI适用于MCAR或MAR机制，不能用于MNAR机制。其优点在于考虑到缺失值的不确定性，提供更为有效且无偏的估计标准误，使得试验结果更加稳健、可靠。研究证实，在缺失机制为MAR的情况下，MI可充分考虑缺失值的不确定性并提供无偏性结果，因此广泛用于处理临床试验中的缺失值[3,22-23]。该方法的缺点在于数据分析比单一插补更为繁琐，工作量更大。若在MNAR机制中错误应用MI方法进行插补，可能引入系统性偏差，导致错误的结果推断。

3.2.3　基于模型插补

基于模型插补是指应用有关数据分布的假设（包括均值和中位数插补）估计缺失值的方法，或假设辅助变量（或x变量）与目标y变量之间的关系，以预测缺失值。该方法在包含缺失值的数据集中为每个目标变量建立一个预测模型，在观测数据上拟合模型，随后生成插补值去填补缺失值。

常见模型包括基于似然方法、模式混合模型、马尔柯夫链蒙特卡罗模型，以及最近热门的期望最大化算法和人工智能方法。诸多学者已对这些方法给出详细解释、示例和模拟结果[15,24-27]。如Cole在研究中采用马尔柯夫链蒙特卡罗模型填补生存质量资料（分类变量结局）中的缺失数据[28]。

基于模型填补方法一般包括4个步骤（图2）：

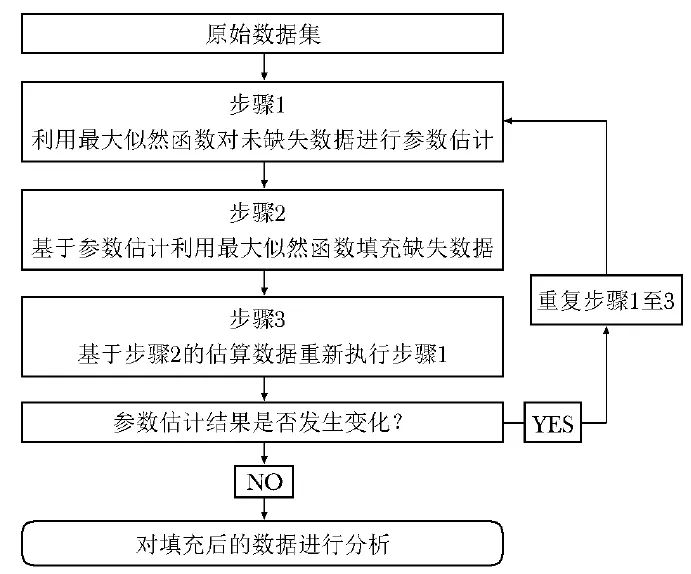
图2 基于模型插补方法流程图

首先，利用最大似然函数对未缺失数据进行参数估计（步骤1）；其次，利用最大似然函数对缺失数据进行估计填补（步骤2）；再次，根据第2步确定的估计填补数据重新进行第1步的参数估计（步骤3）；最后，则是包括步骤1、2和3在内的迭代过程，即步骤4包括重复执行前面三个步骤，直到参数估计结果稳定，无更多变化。

Ratitch等[15]在一项针对重度抑郁者的临床试验中，将25项汉密顿抑郁量表中前17个问题总分的变化作为结果变量，使用模式混合模型估计缺失值，为后续数据分析提供合理的估计结果。

基于模型插补是一种较为复杂的缺失值处理方法，其独特之处在于可在MNAR的假设下分析数据。此方法的优点在于处理缺失值问题时更具稳健性和有效性。然而，由于算法较为复杂，研究者通常需具备较强的统计学知识背景，因此其广泛应用受到一定影响。

3.3 逆概率加权法

IPW是一种基于权重的数据缺失处理方法，其通过对含有缺失数据的参与者分配权重0，无缺失数据的参与者按照非缺失概率的倒数进行加权，从而创造出一个虚拟的新人群（pseudo-population）完整数据集。在部分文献中，IPW可能会被细分为IPW1和IPW2[16]。IPW1通常是一种基于观测数据的加权方法，而IPW2则是一种基于模型的加权方法。通常采用Logistic回归模型计算非缺失概率，其中因变量为非缺失值，协变量为其可能的预测因素。最后仅对含有完整数据的参与者进行加权回归分析，估计干预效果。图3展示了IPW方法的概念性过程。

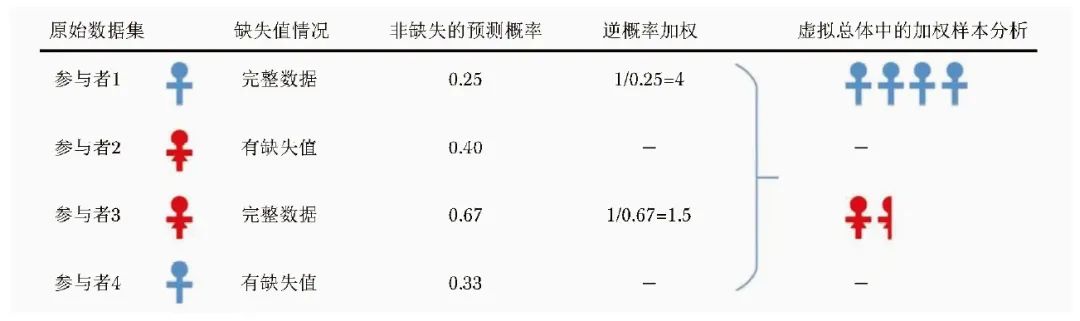
图3 逆概率加权法处理缺失值流程图

Mongin等[16]在一项模拟研究中比较了肿瘤坏死因子抑制剂与另一种作用机制的生物类抗风湿病药物治疗类风湿关节炎患者的有效性，选用了IPW处理缺失值，且与多重插补、完整案例分析等方法进行比较，以1年内低疾病活跃度的估计值为评价指标，结果显示应用完整案例分析和IPW1可高估低疾病活跃度的绝对差异，相反IPW2和多重插补可得出无偏的低疾病活跃度估计值。

IPW适用于MCAR和MAR机制，对于MNAR机制并不适用。其优点在于为不同的样本分配不同的权重以校正样本选择偏差，可选择不同的权重计算方法，具有较高的灵活性。相较于MI，IPW操作更为简单，结果解读也相对容易，无需进行多次插补，且仅涉及1个完整的数据集，是处理缺失值常用的方法之一。IPW的缺点在于对缺失数据较为敏感，若数据缺失比例较高，IPW的权重分配可能受到影响，导致对效应值的估计不准确。此外，该方法需进行一定程度的建模和计算，增加了使用难度。

4 缺失值处理方法的选择及建议

综上，缺失值的处理方法大致分为删除法、插补法和IPW法。其中，删除法操作最简单，但仅适用于MCAR机制，违背了意向性治疗分配（intent-to-treat）原则。相较于删除法，插补法可减少信息损失。单一插补保留了数据集的完整性，简单易行，但忽视了数据的变异程度；MI不仅摒弃了单一插补主要的弊端，且充分考虑到缺失值的不确定性，对标准误的估计和研究结果的推断更具准确性；基于模型插补则可在MNAR机制下有效处理缺失值，运用多种模型填补缺失数据，插补过程更加严谨合理。

但MI和基于模型插补的算法和处理均较为复杂，研究者需具备丰富的统计学知识和计算机操作能力，导致其实际应用受到一定程度的限制。相对而言，IPW法灵活性更高，其操作和结果解读也较为简单，但对缺失数据敏感，也需要复杂的建模和计算。 

目前，尚无公认的最佳缺失值处理方法，不同方法得出的估计值往往有所差别，但再强大的缺失值处理方法都不可能替代充分的试验设计和实施。此外，即使事后填补缺失值，也依然无从得知数据缺失的真实原因，无法评估填补后数据集的结果估算值是否正确。因此，为彻底解决临床试验中的缺失数据问题，最佳方法是在试验过程中防止数据缺失，而非事后试图填补缺失的数据。

在试验设计和实施阶段，为防止缺失值的出现，提出如下建议：

1

研究者可通过电话或电子邮件的方式进行调查，以最大限度减少参与者亲自就诊的次数；

2

为每次随访预设合理的时间，并根据参与者的时间制订灵活的日程安排；

3

在长期随访研究中，为参与者提供激励措施，充分补偿参与者所付出的时间和精力，以增加其参与研究的积极性和依从性；

4

简化调查问卷内容，并选用先进的数据收集工具，作到“精益”数据；

5

为缺失值设定最低限度，若超出预估目标则制订相应的解决方案，了解数据缺失的原因，针对具体缺失原因进行对应的敏感性分析，并遵循相关报告指南等。

5 小结与展望

缺失值处理问题一直是临床试验中备受关注的重要话题。本文阐述了常见的缺失值类型及其处理方法，通过图、表、理论结合实例等多种形式，旨在提高临床科研工作者对缺失值的理解和认识，减少临床试验中缺失值的不当处理和不规范报告。

删除法、插补法和IPW法是常见的缺失值处理方法，各具优劣，只有在满足其要求的缺失机制和特定情境下，方能展现出优势。若不能满足缺失机制假设，无论何种处理方法均可能引入偏倚，而非解决存在的问题。处理缺失值最好的方法是防止数据丢失，为避免或减少临床试验中的数据缺失，需在研究设计和实施等阶段进行全面、科学、严谨的考虑。

参考文献

［1］National Research Council. The prevention and treatment of missing data in clinical trials［M］. Washington, D.C.: The National Academies Press, 2010.

［2］Häckl S, Koch A, Lasch F. Empirical evaluation of the implementation of the EMA guideline on missing data in confirmatory clinical trials: specification of mixed models for longitudinal data in study protocols［J］. Pharm Stat, 2019, 18(6): 636-644.

［3］Austin P C, White I R, Lee D S, et al. Missing data in clinical research: a tutorial on multiple imputation［J］. Can J Cardiol, 2021, 37(9): 1322-1331.

［4］Marino M, Lucas J, Latour E, et al. Missing data in primary care research: importance, implications and approaches［J］. Fam Pract, 2021, 38(2): 200-203.

［5］Altman D G. Missing outcomes in randomized trials: addressing the dilemma［J］. Open Med, 2009, 3(2): e51-e53.

［6］Groenwold R H H, Moons K G M, Vandenbroucke J P. Randomized trials with missing outcome data: how to analyze and what to report［J］. CMAJ, 2014, 186(15): 1153-1157.

［7］Bell M L, Fiero M, Horton N J, et al. Handling missing data in RCTs; a review of the top medical journals［J］. BMC Med Res Methodol, 2014, 14: 118.

［8］何丽云, 刘保延, 梁志伟, 等. 临床研究中数据管理及其质量评价［J］. 中国新药与临床杂志, 2005, 24(11): 916-919.

［9］Lazar N A. Statistical analysis with missing data［J］. Technometrics, 2003, 45(4): 364-365.

［10］Heymans M W, Twisk J W R. Handling missing data in clinical research［J］. J Clin Epidemiol, 2022, 151: 185-188.

［11］Rautenberg T A, Ng S K, George G, et al. Seemingly unrelated regression analysis of the cost and health-related quality of life outcomes of the REVAMP randomized clinical trial［J］. Value Health Reg Issues, 2023, 35: 42-47.

［12］Sayasone S, Keiser J, Meister I, et al. Efficacy and safety of tribendimidine versus praziquantel against Opisthorchis viverrini in Laos: an open-label, randomised, non-inferiority, phase 2 trial［J］. Lancet Infect Dis, 2018, 18(2): 155-161.

［13］Menendez M E, Thornton E, Kent S, et al. A prospective randomized clinical trial of prescription of full-time versus as-desired splint wear for de Quervain tendinopathy［J］. Int Orthop, 2015, 39(8): 1563-1569.

［14］Witkiewitz K, Falk D E, Kranzler H R, et al. Methods to analyze treatment effects in the presence of missing data for a continuous heavy drinking outcome measure when partici-pants drop out from treatment in alcohol clinical trials［J］. Alcohol Clin Exp Res, 2014, 38(11): 2826-2834.

［15］Ratitch B, O'Kelly M, Tosiello R. Missing data in clinical trials: from clinical assumptions to statistical analysis using pattern mixture models［J］. Pharm Stat, 2013, 12(6): 337-347.

［16］Mongin D, Lauper K, Finckh A, et al. Accounting for missing data caused by drug cessation in observational compara-tive effectiveness research: a simulation study［J］. Ann Rheum Dis, 2022, 81(5): 729-736.

［17］Tsikriktsis N. A review of techniques for treating missing data in OM survey research［J］. J Oper Manag, 2005, 24(1): 53-62.

［18］Lachin J M. Fallacies of last observation carried forward analyses［J］. Clin Trials, 2016, 13(2): 161-168.

［19］衡明莉, 陈丽嫦, 王骏. 临床试验中缺失数据处理方法研究［J］. 中国临床药理学杂志, 2019, 35(22): 2948-2952.

［20］Rubin D B. A method for formalizing subjective notions about the effect of non-respondents in sample surveys［J］. ETS Res Bull Ser, 1975, 1975(2): i-24.

［21］Rubin D B. Multiple imputation for nonresponse in surveys［M］. New York: John Wiley & Sons, Inc., 1987.

［22］Schafer J L. Multiple imputation: a primer［J］. Stat Methods Med Res, 1999, 8(1): 3-15.

［23］De Goeij M C M, Van Diepen M, Jager K J, et al. Multiple imputation: dealing with missing data［J］. Nephrol Dial Transplant, 2013, 28(10): 2415-2420.

［24］Fairclough D L, Peterson H F, Cella D, et al. Comparison of several model-based methods for analysing incomplete quality of life data in cancer clinical trials［J］. Stat Med, 1998, 17(5/7): 781-796.

［25］Enders C K, Du H, Keller B T. A model-based imputation procedure for multilevel regression models with random coefficients, interaction effects, and nonlinear terms［J］. Psychol Methods, 2020, 25(1): 88-112.

［26］Kim S, Sugar C A, Belin T R. Evaluating model-based imputation methods for missing covariates in regression models with interactions［J］. Stat Med, 2015, 34(11): 1876-1888.

［27］Tseng C H, Chen Y H. Regularized approach for data missing not at random［J］. Stat Methods Med Res, 2019, 28(1): 134-150.

［28］Cole B F, Bonetti M, Zaslavsky A M, et al. A multistate Markov chain model for longitudinal, categorical quality-of-life data subject to non-ignorable missingness［J］. Stat Med, 2005, 24(15):2317-2334.